Banach Space Prove That There is No Continuous Path That Connects T With the Identity Operator

Introduction

In this paper we present three global bifurcation results for critical values of $C^1$ maps in Banach spaces and of $C^{2}$ maps in Hilbert spaces. We proceed in the general spirit of the family of works that uses topological methods, whose origin can be found in the textbook of Krasnoselskij [19] in 1964 and the paper of Rabinowitz [25] in 1971, even though, we must emphasize, their results concern bifurcation of solutions of particular equations, while ours are related to bifurcation of critical values, that is, target values of a particular function.

Krasnoselskij obtains the following local bifurcation theorem, which we recall in a simplified version. Let X be a real Banach space. Consider a map $f:\mathbb R\times X\rightarrow X$ of the form

$$\begin{aligned} f(\lambda ,x)=x-\lambda C(x), \end{aligned}$$

where C is nonlinear, compact, Fréchet differentiable at $x=0$ and such that $C(0)=0$. We use the term "compact" for a continuous map sending bounded subsets of the domain to relatively compact subsets of the target space. The solutions of the equation

$$\begin{aligned} f(\lambda ,x)=0 \end{aligned}$$

(1.1)

of the form $(\lambda ,0)$ are called trivial, and a real number $\lambda _0$ is called a bifurcation point of (1.1) if every neighborhood of $(\lambda _0,0)$ in $\mathbb R\times X$ contains nontrivial solutions. It is immediate to notice that a necessary condition for $\lambda _0$ to be a bifurcation point is that the linear operator $Id-\lambda _0C'(0)$ is not invertible, that is, $\lambda _0$ is a characteristic value of the Fréchet derivative $C'(0)$ of C at zero (which is a compact linear operator).

Krasnoselskij proves that $\lambda _0$ is a bifurcation point of (1.1) if it is a characteristic value of $C'(0)$ of odd algebraic multiplicity. Rabinowitz extends this result, proving a so-called global bifurcation theorem, i.e., showing that there exists a connected set R of nontrivial solutions whose closure contains $(\lambda _0,0)$ and such that at least one of the two alternatives is verified:

(i)
R is unbounded,
(ii)
the closure of R meets a point of the form $(\lambda _1,0)$ with $\lambda _0\ne \lambda _1$.

It is obvious why Krasnoselskij's result is usually called local, while Rabinowitz's one global. The approaches of the two authors are based on the application of the Leray–Schauder degree. It is not possible to explain here such a method in details. We limit ourselves to recall the following idea: take $\lambda \in \mathbb R$. If $Id-\lambda C'(0)$ is an automorphism of X, we simply denote by the symbol $\deg _{\mathrm{LS}}(Id-\lambda C'(0))$ the Leray–Schauder degree of the triple $(Id-\lambda C'(0), U,0)$, where U is any open bounded subset of X containing the origin. Such a value could be 1 or $-1$, while the Leray–Schauder degree of any triple $(Id-\hat{\lambda }C'(0),U,0)$ is not defined when $\hat{\lambda }$ is a characteristic value of $C'(0)$. The degree is also locally constant, when defined, with respect to $\lambda $. It can be proven that, when $\lambda $ crosses a characteristic value $\hat{\lambda }$, the number $\deg _{\mathrm{LS}}(Id-\lambda C'(0))$ changes sign if and only if $\hat{\lambda }$ has odd algebraic multiplicity. This sign jump guarantees the bifurcation at $\hat{\lambda }$. If, otherwise, the algebraic multiplicity of $\hat{\lambda }$ is even, this point could be (or not) a bifurcation point, but the degree does not help to give an answer.

Now, two interesting facts happen:

(a)
If, in Eq. (1.1), X is a real separable Hilbert space and $C'(0)$ is a symmetric (i.e., self-adjoint) operator, then every characteristic value of $C'(0)$ is a bifurcation point;
(b)
In some cases, the bifurcation points that are characteristic values of $C'(0)$ of even algebraic multiplicity do not produce a "global bifurcation branch" in the sense of Rabinowitz's theorem.

Some questions have been quite naturally stimulated in the last decades and in recent years by the above facts: if one tackles a more general problem than (1.1), is it possible to find a more general degree theory to detect local or global bifurcation? Can we use more sophisticated topological methods than degree theories? How can we explain that, in some cases, there is local and not global bifurcation?

More general topological degree theories have been introduced, extending the Leray–Schauder degree to compact and noncompact perturbations—also multivalued perturbations—of nonlinear Fredholm maps between Banach spaces (see, e.g., [5,6,7, 11, 12, 14, 15, 21, 24, 30]). Consequently, local and global bifurcation results have been obtained for more general problems than (1.1). Actually there is an enormous literature on the subject.

Consider for example a Banach space X and a $C^1$ map $f:\mathbb R\times X\rightarrow X$. Assume $f(\lambda ,0)=0$ for $\lambda \in \mathbb R$. Suppose that, for any $(\lambda ,x)$, the Fréchet derivative $\partial _2f(\lambda ,x)$ of f with respect to the second variable at $(\lambda ,x)$ is a Fredholm operator of index zero. With a particular notion of orientation for Fredholm maps in (possibly infinite dimensional) Banach spaces, it is possible to define a topological degree for any partial map $f(\lambda ,\cdot )$ (see [6, 13, 15]). Given $\lambda \in \mathbb R$, denote by $L_{\lambda }$ the operator $\partial _2f(\lambda ,0)$. Suppose $\lambda _0$ is such that $L_{\lambda }$ is an isomorphism for $\vert \lambda -\lambda _0\vert $ small and nonzero. If the degree of $L_{\lambda }$ has a sign jump when $\lambda $ crosses $\lambda _0$, then $\lambda _0$ turns out to be a bifurcation point of $f(\lambda ,x)=0$ with a global bifurcation behavior. Analogously to the case of compact perturbations of the identity studied by Krasnoselskij and Rabinowitz, also in this case the lack of sign jump of the degree does not say anything about bifurcation.

In the self-adjoint case, the Morse index is a useful tool to detect local bifurcation (but not global, see the above remark b) in some cases for which the degree does not help. Consider a separable real Hilbert space H. It is known that, given a self-adjoint Fredholm operator $T:H\rightarrow H$, there exists a unique orthogonal splitting of H,

$$\begin{aligned} H=V^-(T)\oplus V^+(T)\oplus \ker T, \end{aligned}$$

such that $V^-(T)$ and $V^+(T)$ are T-invariant, the quadratic form $x\mapsto \langle Tx,x\rangle $ is negative definite on $V^-(T)$ and positive definite on $V^+(T)$.

With a slight abuse of notation, we will refer to $V^-(T)$ and $V^+(T)$ as the negative and the positive eigenspaces of T, respectively. The Morse index of T, denoted by $\mu (T)$, is defined as the dimension of $V^-(T)$ when it is finite. The following local bifurcation result can be found in the textbook [22] by Mawhin and Willem (see also [16, 26]). They consider a compact interval [a,b] and an open neighborhood U of $[a,b]\times \{0\}$ in $\mathbb R\times H$. Given a $C^{2}$ map $\psi :U\rightarrow \mathbb R$, denote by $L_{\lambda }$ the Hessian of $\psi _{\lambda }:=\psi (\lambda ,\cdot )$ at zero, that is, the second derivative of $\psi $ with respect to second variable at the point $(\lambda ,0)$.

Theorem A

In the above notation, assume that $0\in H$ is a critical point of the functional $\psi _{\lambda }$ for every $\lambda \in [a,b]$. In addition, assume that $L_{\lambda }:H\rightarrow H$ is a Fredholm operator and suppose that the negative eigenspace $V^-(L_{\lambda })$ is finite dimensional for every $\lambda \in [a,b]$. If

$$\begin{aligned} \mu (L_{a})\ne \mu (L_{b}), \end{aligned}$$

then the interval [a,b] contains a bifurcation point.

The above important result does not apply in the important case when the operators $L_{\lambda }$ are so-called strongly indefinite, that is, when their positive and negative eigenspaces have infinite dimension. In order to extend Theorem A to the strongly indefinite case, in a series of papers by Fitzpatrick et al. [16, 17, 23] a bifurcation problem for a Hamiltonian system is investigated by the application of the spectral flow. The spectral flow has been introduced by Athiyah et al. [3], and it is a topologically invariant integer number associated with a continuous path of self-adjoint Fredholm operators, $L_\lambda $, $\lambda \in [a,b]$, in a separable real Hilbert space H. The spectral flow can be defined by different equivalent methods. In the next section we will summarize its construction, following the approach of Fitzpatrick et al. [16]. Here, we limit ourselves to observe that

$$\begin{aligned} {\text {sf}}(L,[a,b]) = \mu (L_{a})-\mu (L_{b}) \end{aligned}$$

when both sides of the above equality are meaningful. In [16] it is proven the following extension of Theorem A.

Theorem B

(Fitzpatrick, Pejsachowicz, Recht) Let H be a separable real Hilbert space and let $\psi :\mathbb R\times H \rightarrow \mathbb R$ be a $C^2$ function such that, for each $\lambda \in \mathbb R$, $x=0$ is a critical point of the functional $\psi _{\lambda }:=\psi (\lambda ,\cdot )$. Assume that the Hessian $L_{\lambda }$ of $\psi _{\lambda }$ at 0 is Fredholm and that $L_{a}$ and $L_{b}$ are nonsingular for suitable a,b. If ${\text {sf}}(L, [a, b])\ne 0$, then every neighborhood of $[a, b]\times \{0\}$ contains points $(\lambda , x)$ such that x is a nonzero critical point of $\psi _{\lambda }$.

Formula (1.2) gives an interesting algebraic relation between the spectral flow and the Leray–Schauder degree and helps to understand why Theorems B (and also Theorem A) improves Krasnoselskij's local bifurcation result. If $L_\lambda $, $\lambda \in [a,b]$, is a continuous path of self-adjoint Fredholm operators in a separable real Hilbert space H, and $L_{\lambda }$ is of the form

$$\begin{aligned} L_{\lambda }=Id-K_{\lambda }, \end{aligned}$$

where Id is, as previously, the identity and any $K_{\lambda }$ is symmetric and compact, then one can prove (see [16]) that

$$\begin{aligned} (-1)^{{\text {sf}}(L, [a, b])}=\deg _{\mathrm{LS}}(L_{a})\cdot \deg _{\mathrm{LS}}(L_{b}). \end{aligned}$$

(1.2)

The above equality explains why the spectral flow is a finer invariant than the degree to detect bifurcation, even if it can be applied in a more restricted context. The spectral flow could be nonzero with a lack of sign jump of the degree. In other words, it detects bifurcation in some cases when the degree does not.

On the other hand, the spectral flow helps to prove local bifurcation results, as in Theorem B, and it seems unable to provide global bifurcation results. The reason is probably due to the fact that the spectral flow is defined for linear operators, while the degree works in nonlinear maps (see Example 3.5). A possible nonlinear version of the spectral flow could help to obtain global bifurcation results, but to the best of our knowledge it does not exist, and its construction (if possible) is an interesting and challenging open problem.

Motivated by these difficulties and, at the same time, by the purpose of studying global bifurcation, in this paper we face a different problem focusing our attention on bifurcation of target values of a suitable function. One of the results we present in this paper, Theorem 3.3, shows the existence of a global bifurcation branch of critical values of a $C^1$ map $f : \mathbb R\times X \rightarrow \mathbb R$, where X is a real Banach space and some topological conditions are verified. It includes, as a second result, the particular case in which X is a separable Hilbert space, f is $C^2$, the Hessians of f with respect to the second variable at the points $(\lambda ,0)$,

$$\begin{aligned} L_\lambda :=\dfrac{\partial ^2f}{\partial x^2}(\lambda ,0):H\rightarrow H, \end{aligned}$$

are Fredholm, and a sufficient condition to obtain bifurcation is given in terms of Morse index (Theorem 3.4). We also obtain a third global bifurcation result, Theorem 6.1, also for the $C^2$ case, when the Hessians $L_\lambda $ are strongly indefinite and the Morse index is not defined. Adding a particular compactness assumption, which at this moment we are not able to remove, we prove a global bifurcation result if the spectral flow of $L_\lambda $ in a suitable interval is nonzero. Theorem 6.1 clearly draws inspiration from the seminal papers [16, 17] by Fitzpatrick, Pejsachowicz and Rabier and uses the spectral flow in a context of a global bifurcation problem.

In our first theorem, we obtain the bifurcation result assuming that two suitable topological pairs of inverse images of the map $f_{\lambda }$ are not homotopy equivalent, for two different values of the parameter $\lambda $. This condition is sufficient to give bifurcation when combined with other assumptions (see below), such as a special Palais–Smale-type condition.

The paper is organized as follows. In Sect. 2 we recall some basic notions of homotopy equivalence of topological pairs and we summarize the construction of the spectral flow. In Sect. 3 we present the bifurcation problem and we state our main results, Theorems 3.3 and 3.4. In Sect. 4 we show some technical results concerning deformation of level sets, which are used in the proofs of our main results. Such deformation results are original and have in our opinion some independent interest. Section 5 is devoted to the proof of Theorems 3.3 and 3.4. In Sect. 6 we provide a bifurcation theorem for strongly indefinite functionals where the corresponding invariant for the Hessian is the spectral flow. Finally, in Sect. 7 we illustrate the applicability of Theorem 3.4 with a second-order ODE.

Preliminaries

First of all, let us summarize the construction of the spectral flow in the approach followed by Fitzpatrick et al. [16]. Let H be an infinite-dimensional separable real Hilbert space. Consider an orthogonal decomposition

$$\begin{aligned} H=H_{+}\oplus H_{-}, \end{aligned}$$

(2.1)

with $H_{+}$ and $H_{-}$ of infinite dimension. We call symmetry the linear operator $\mathcal {J}:H\rightarrow H$ which can be represented, in splitting (2.1), by the block matrix of operators

$$\begin{aligned} \left( \begin{array}{ll} Id_{H_{+}} &{} 0\\ 0 &{} - Id_{H_{-}} \end{array}\right) . \end{aligned}$$

Observe that we have infinitely many symmetries of H, depending on splittings like (2.1), and that $\mathcal {J}^{2}=Id$ for any symmetry $\mathcal {J}$. Let $\{e_{n}^{{\pm }}, \; n\in \mathbb N\}$ be two Hilbert bases of $H_{+}$ and $H_{-}$, respectively, and call $H_{n}$ the 2n-dimensional subspace of H generated by $\{e_{k}^{{\pm }}, \; k\le n\}$. Denote by $P_{n}:H\rightarrow H_{n}$ the orthogonal projection. Given a self-adjoint compact linear operator $K:H\rightarrow H$, consider $L=\mathcal {J}+K$. Let $L_{n}:H_{n}\rightarrow H_{n}$ be the operator given by

$$\begin{aligned} L_{n}x=P_{n}(Lx) \end{aligned}$$

and call signature of $L_{n}$ the integer number

$$\begin{aligned} {\text {sign}}L_{n}=\mu (-L_{n})-\mu (L_{n}), \end{aligned}$$

where, as already said, $\mu (\cdot )$ is the Morse index of the considered operator. In [16, Lemma 1.1] the following result is proven.

Lemma

(Fitzpatrick, Pejsachowicz, Recht) Suppose that $L=\mathcal {J}+K$ is an automorphism of H. Then, there is a positive integer N such that ${\text {sign}}L_{n}$ is constant if $n\ge N$.

The above eventually constant integer is called generalized signature of L with respect to $\mathcal {J}$ and is denoted by ${\text {sign}}_{\mathcal {J}}(L)$. It is possible to prove that this integer actually depends on the symmetry $\mathcal {J}$ (as the notation suggests), but not on the chosen Hilbert bases $\{e_{n}^{{\pm }}\}$ of the subspaces of H related to $\mathcal {J}$. In other words, even if the definition of any $L_n$ clearly depends on the chosen bases $\{e_{n}^{{\pm }}\}$, one can prove that ${\text {sign}}_{\mathcal {J}}(L)$ does not.

Consider now a continuous path $K_{\lambda }$, $\lambda \in [a,b]$, of self-adjoint compact operators of H. Given a symmetry $\mathcal {J}$ of H, take the path $L_{\lambda }=\mathcal {J}+K_{\lambda }$ and suppose that $L_{a}$ and $L_{b}$ are automorphisms. The spectral flow of the path L is defined as

$$\begin{aligned} {\text {sf}}(L,[a,b])= \dfrac{{\text {sign}}_{\mathcal {J}}(L_{b})-{\text {sign}}_{\mathcal {J}}(L_{a})}{2}. \end{aligned}$$

(2.2)

One can prove that the above formula does not depend on $\mathcal {J}$ even though ${\text {sign}}_{\mathcal {J}}(L_{a})$ and ${\text {sign}}_{\mathcal {J}}(L_{b})$ do. The definition of spectral flow can be extended to any continuous path of self-adjoint Fredholm operators $L_{\lambda }$, $\lambda \in [a,b]$, such that $L_{a}$ and $L_{b}$ are invertible. In the particular case when $L_\lambda = T + K_\lambda $, where T is Fredholm and self-adjoint, and any $K_\lambda $ is compact and self-adjoint, the spectral flow is defined as

$$\begin{aligned} {\text {sf}}(L, [a, b]) = \dim (V^-(L_a) \cap V^+(L_b)) - \dim (V^-(L_b) \cap V^+(L_a)), \end{aligned}$$

(2.3)

which is finite. In the case of a general path of self-adjoint Fredholm operators $L_\lambda $, it can be proven the existence of a path $M_\lambda $ of automorphisms of H (called cogredient parametrix) such that

$$\begin{aligned} M_\lambda ^*L_\lambda M_\lambda = T + K_\lambda , \end{aligned}$$

where $M_\lambda ^*$ is the adjoint of $M_\lambda $, T is Fredholm and self-adjoint and any $K_\lambda $ is compact and self-adjoint. Hence, the definition ${\text {sf}}(L, [a, b])$ is given by (2.3) applied to $T + K_\lambda $ and this does not depend on the choice of $M_\lambda $. The reader can see [16] for an accurate study of the properties of the spectral flow.

We now recall a basic definition of homotopy theory. Consider a pair of topological spaces, that is, a pair (X,A) such that X is any topological space and $A\subseteq X$. Given a continuous map $F:X\rightarrow Y$ between topological spaces, to simplify the notation and avoid the introduction of new symbols, we will denote by $F:(X,A) \rightarrow (Y,B)$ the corresponding continuous maps between pairs (if, of course, it is well defined, that is, if $F(A)\subseteq B$).

Two functions $F,G:(X,A) \rightarrow (Y,B)$ are homotopic if there exists a continuous map $H:[0,1] \times X \rightarrow Y$ such that $H(0,x) = F(x),\; H(1,x) = G(x)$ and $H(t, x) \in B$ for all $x\in A$ and all $t\in [0,1]$. Two pairs (X,A) and (Y,B) are homotopy equivalent if there exist two maps $F:(X, A) \rightarrow (Y,B)$ and $G:(Y,B) \rightarrow (X,A)$ such that $G\circ F$ and $F \circ G$ are homotopic to the identity (in the sense described above). If this is the case, we have isomorphisms in the relative homology groups $H_i(X,A) \cong H_i(Y,B)$ for every i, see for example [18, pag. 118]. We consider here singular homology groups with coefficients in $\mathbb R$.

Let now X be a real Banach space. Consider a $C^{1}$ function $\varphi :X \rightarrow \mathbb R$, an isolated critical point p of $\phi $ and any $k \in \mathbb N$. Denote $c=\phi (p)$ and let $\phi ^{(c)} $ be the set $\{x\in X: \phi (x)\le c\}$. Following Chang [9] (see also [22]), we define the kth-local critical group $C_k(\varphi ,p)$ as

$$\begin{aligned} C_k(\varphi ,p):=H_{k}\left( \phi ^{(c)}\cap U,(\phi ^{(c)}\setminus \{p\})\cap U\right) \end{aligned}$$

(2.4)

where, as previously, we consider here singular homology with coefficients in $\mathbb R$. The set U is an open neighborhood of p not containing any other critical point of $\phi $. Let us point out that, by general properties in singular homology theory, the above definition does not depend on U.

As we will see, the key ingredient to prove local bifurcation of critical points is the invariance of the critical groups under small perturbations. The next theorem is proven in [22, Section 8.9].

Theorem 2.1

Let U be an open neighborhood of a given point v in a Hilbert space H and consider a map $\varphi \in C^{2}(U,\mathbb R)$ having v as the only critical point and satisfying the Palais–Smale condition over a closed ball $B(v,r) \subseteq U$. Then, there exists $\eta > 0$, depending only upon $\varphi $, such that, for any $\psi $ satisfying the same assumptions, the condition

$$\begin{aligned} \sup _{u \in U}(|\psi (u)-\varphi (u)|) + (|\nabla \psi (u)-\nabla \varphi (u)|) \le \eta \end{aligned}$$

implies

$$\begin{aligned} \dim C_k(\psi , v) = \dim C_k(\varphi , v), \quad k \in \mathbb N. \end{aligned}$$

As a consequence, if a function f as in Theorem A has nonvanishing spectral flow in the interval [a,b], then we have

$$\begin{aligned} \dim C_k(f_a, 0) \ne \dim C_k(f_b, 0) \end{aligned}$$

and thus $0 \in X$ cannot be isolated as a critical point for every $\lambda $.

We will consider a global version of the local critical groups explained by Theorem 2.2 that can be found in [9, Theorem 5.1.27].

Theorem 2.2

Let X be a real Banach space. Assume that $\varphi : X \rightarrow \mathbb R$ is $C^1$ and satisfies the Palais–Smale condition. Suppose that c is an isolated critical value of $\varphi $, where the critical points of $\varphi $ in $\varphi ^{-1}(c)$ are $z_1, \ldots , z_m$. Then for sufficiently small $\varepsilon > 0$ we have

$$\begin{aligned} H_k\left( \varphi ^{(c+\varepsilon )} , \varphi ^{(c-\varepsilon )} \right) = \bigoplus _{j=1}^m C_k(\varphi , z_j) \end{aligned}$$

for every $k = 0,1,2, \ldots $

Theorem 2.2 plays a central role in the proof of our main results.

Main results

Let us start by presenting the following conditions which will be considered throughout the paper.

Definition 3.1

Let X be a real Banach space. We say that a $C^{1}$ map $f :\mathbb R\times X \rightarrow \mathbb R$ satisfies the basic condition if

$$\begin{aligned} f(\lambda ,0) = 0 \quad \text {and} \quad \frac{\partial f}{\partial x} (\lambda ,0) =f'_\lambda (0)= 0, \quad \forall \lambda \in \mathbb R. \end{aligned}$$

(3.1)

The map $x\in X\mapsto f(\lambda ,x)$, defined for a given real $\lambda $, will be also denoted by $f_{\lambda }$ and its Fréchet derivative at a point x by $f'_\lambda (x)$. The following subset of $\mathbb R^2$

$$\begin{aligned} S_f = \{(\lambda , y) \in \mathbb R^2 : f_\lambda (x) = y,\ f'_\lambda (x) = 0 \hbox { for some } x \in X\} \end{aligned}$$

will be called the set of critical pairs. In other words, $S_f$ is the set of pairs $(\lambda , y)$ such that y is a critical value of $f_\lambda $. The line $Z = \mathbb R\times \{0\} \subseteq S_f$ is regarded as the set of the trivial critical pairs. We say that a trivial critical pair $(\lambda _{0},0) \in Z$ is a bifurcation point if every neighborhood of $(\lambda _{0},0)$ contains nontrivial critical pairs. Then, we see that

$$\begin{aligned} E_f := \overline{S_f \setminus Z} \end{aligned}$$

(3.2)

is the union of the bifurcation points and the nontrivial critical pairs. We will also consider a subset of trivial critical pairs:

$$\begin{aligned} Z_{{\text {in}}}= [-1,1] \times \{0\} \subset \mathbb R^2. \end{aligned}$$

(3.3)

Definition 3.2

((PS)-type conditions). Let $I \subset \mathbb R$ be a compact interval and $c\in \mathbb R$ be given. We say that f satisfies the $({\text {PS}})_{I,c}$ condition if, for every sequence $(\lambda _n, x_n)$ in $I \times X$ such that $f_{\lambda _n}(x_n) \rightarrow c$ and such that $f_{\lambda _n}'(x_n) \rightarrow 0 \in X^*$, there exists a subsequence $(x_{n_k})$ converging to a point $ x_0 \in X$.

Let J be a subset of $\mathbb R$. We say that f satisfies the $({\text {PS}})_{I,J}$ condition if it satisfies the $({\text {PS}})_{I,c}$ condition for every $c \in J$. We say that f satisfies the $({\text {PS}})_{\mathbb R,\mathbb R}$ condition if it satisfies the $({\text {PS}})_{[-N,N],\mathbb R}$ condition for every $N \in \mathbb N$.

We are now in a position to state the following two theorems which, associated with Theorem 6.1, are our main results. Actually, Theorem 3.4 is a consequence of Theorem 3.3, particularly important in applications. The proof of both results is given in Sect. 5.

Theorem 3.3

Let $f : \mathbb R\times X \rightarrow \mathbb R$ be a $C^1$ function verifying basic condition (3.1). Denote by $\partial _1 f: \mathbb R\times X \rightarrow \mathbb R$ the map

$$\begin{aligned} \partial _1 f(\lambda , x) = \frac{\partial f}{\partial \lambda }(\lambda , x). \end{aligned}$$

Assume that the following conditions hold:

(i)
f satisfies the $({\text {PS}})_{\mathbb R,\mathbb R}$ condition.
(ii)
$\partial _1 f$ is bounded in the sets of the form

$$\begin{aligned} f_{[-N,N]}^{-1}([-N,N]):=\{(\lambda ,x)\in [-N,N] \times X: f(\lambda ,x)\in [-N,N]\}, \quad \forall N \in \mathbb N. \end{aligned}$$
(iii)
The trivial critical pairs $(-1,0), (1,0)$ are not bifurcation points of f.
(iv)
There exists $\varepsilon _* > 0$ such that for every $0< \varepsilon < \varepsilon _*$ the pairs of spaces $\left( f_{-1}^{(\varepsilon )} , f_{-1}^{(-\varepsilon )} \right) $ and $\left( f_1^{(\varepsilon )} , f_1^{(-\varepsilon )} \right) $ are not homotopy equivalent.

Then, $E_f$ contains a connected subset intersecting $Z_{{\text {in}}}$ which either

1.
is unbounded in $\mathbb R^2$, or else
2.
intersects $\{-1,1\} \times \mathbb R$.

Theorem 3.4

Let H be a separable real Hilbert space and consider a $C^2$ function $f : \mathbb R\times H \rightarrow \mathbb R$ satisfying basic condition (3.1).

Denote by I the interval $ [-1,1]$ and assume that the following assumptions hold:

(i)
f satisfies the $({\text {PS}})_{\mathbb R,\mathbb R}$ condition.
(ii)
$\partial _1 f$ is bounded in the sets of the form $f_{[-N, N]}^{-1}([-N, N])$ for every $N \in \mathbb N$.
(iii)
For $i = -1,1$, the point $0 \in H$ is a nondegenerate critical point and the only critical point of $f_i$ with value 0.
(iv)
Assume that, for every $\lambda \in I$, the Hessian of f at zero

$$\begin{aligned} L_\lambda :=\dfrac{\partial ^2f}{\partial x^2}(\lambda ,0):H\rightarrow H \end{aligned}$$

is Fredholm and suppose

$$\begin{aligned} \mu (L_{-1}) \ne \mu (L_1). \end{aligned}$$

where $\mu $ denotes the Morse index. Here we assume that $\mu (L_{-1})$ and $\mu (L_1) $ are finite.

Then the conclusion of Theorem 3.3 holds.

One may ask whether the above theorems work with critical points instead of critical values, as in the bifurcation theorems of Rabinowitz [25]. The answer is negative as proven by R. Böhme [8] (see also [1, 28]). We directly construct, and show below, a counterexample regarding this lack of global behavior in the conditions of Theorem 3.4.

Example 3.5

A classic problem in analysis consists in proving the existence of a cone eversion. This is a smooth function $c:I \times C \rightarrow \mathbb R$, where

$$\begin{aligned} I=[-1,1], \quad \quad C=\{x \in \mathbb R^2 : 1\le \Vert x\Vert \le 2\}, \end{aligned}$$

such that

$$\begin{aligned} c(-1,x) = {\Vert x\Vert }, \ \ c(1,x) = - {\Vert x\Vert } \end{aligned}$$

and such that $c_\lambda $ has no critical points in C for $\lambda \in I$. The existence of such a function may seem counterintuitive but actually is guaranteed by the parametric holonomic approximation theorem, see Example 4.1.1 in [10]. An explicit formula for c was computed in [27]. Taking $\mathbb R^{2}$ as the Hilbert space H in Theorem 3.4, we construct $f :\mathbb R\times \mathbb R^2 \rightarrow \mathbb R^2$ as follows.

The formula for c in polar coordinates as given in [27] is

$$\begin{aligned} c(\lambda , (\alpha , r)) = 2t + g(\lambda , \alpha ) + (r-2) h(\lambda , \alpha ) \end{aligned}$$

for two functions g,h satisfying

$$\begin{aligned} \left( \frac{\partial g}{\partial \alpha }(\lambda , \alpha ), h(\lambda , \alpha )\right) \ne (0,0) \end{aligned}$$

for all $(\lambda , \alpha )$. Given $a,b\in \mathbb R$, consider $p_{a,b}(r) = (3 a-b+1)r^2 + (-2 a+b-2)r^3 +r^4$, which is the polynomial function satisfying the properties

$$\begin{aligned} p_{a,b}(0)=p_{a,b}'(0) = 0, \quad p_{a,b}(1)=a,\quad p'_{a,b}(1)=b, \end{aligned}$$

and define

$$\begin{aligned} f(\lambda , (\alpha , r) ) = p_{g(\lambda , \alpha ), 3 h(\lambda , \alpha )}( r ). \end{aligned}$$

Putting, as usual, $f_{\lambda }:=f(\lambda ,\cdot )$, we easily verify

(i)
$f(\lambda , x), \; \nabla f_{\lambda }(x) \rightarrow +\infty $ uniformly in $\lambda $, as $\Vert x\Vert \rightarrow \infty $.
(ii)
$f(\lambda , 0) = 0, \; \nabla f_{\lambda }(0) = 0$ for all $\lambda \in I$.
(iii)
$f(-1,(\alpha , r) ) = 4 r^2 - 3 r^3 + r^4, f(1,(\alpha , r)) = -2 r^2 - r^3 + r^4$.
(iv)
$\nabla f_{\lambda }(x)\ne 0$ for $\Vert x\Vert = 1$, $\lambda \in I$.

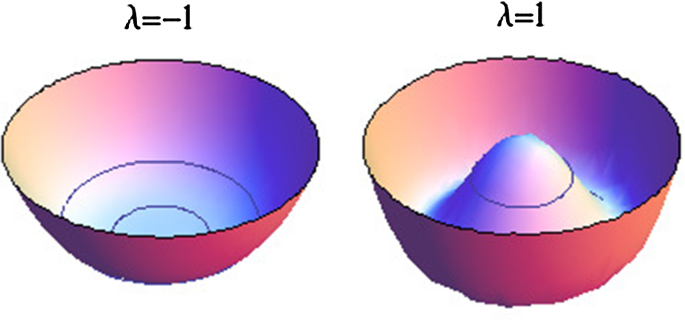
Property (iii) implies

$$\begin{aligned} \mu \left( \dfrac{\partial ^2f}{\partial x^2}(-1,0)\right) =0 \quad \text {and} \quad =\mu \left( \dfrac{\partial ^2f}{\partial x^2}(1,0)\right) =2. \end{aligned}$$

In addition, the path $\lambda \mapsto \nabla f_{\lambda }(0)$ does not satisfy the necessary hypothesis for the "classical" global bifurcation theorem (in the sense of Rabinowitz). Also, one may check that f is in the conditions of Theorem 3.3. Let

$$\begin{aligned} K_f = \{(\lambda , x) \in I \times X : \nabla f_\lambda (x) = 0\} \end{aligned}$$

and notice that condition (iv) forces $K_f \cap (I \times \partial B(0,1)) = \emptyset $. Then, the connected component of $\overline{K_f \setminus (I \times \{0\})}$ containing bifurcation points $(\lambda , 0)$ belongs $I \times B(0,1)$ and does not intersect the subspaces $\lambda = -1,1$. That is, there is local but not global bifurcation.

The function $f_1$ has a set of nontrivial critical points in X of the form $\partial B(0,R)$ with $R \in (1,2)$. Actually the connected component of $K_f$ containing $\{1\}\times \partial B(0,R)$ lies outside $I \times B(0,1)$, but its image by f crosses the value 0.

This example shows that it is not possible to prove global bifurcation of critical points relying only on the fact that the Morse index is nonconstant of Morse index (and, in the infinite-dimensional case, nonvanishing spectral flow).

The proofs of Theorems 3.3 and 3.4 require several lemmas. We start with some results concerning the level sets and the $({\text {PS}})_{I,c}$ condition.

Deformation theorems

We present here some technical lemmas which will play a fundamental role in the proof of Theorems 3.3 and 3.4. Next lemma is a sort of characterization of the $({\text {PS}})_{I,c}$ property. In this section, I denotes a real compact interval and the function f is not required to verify basic condition (3.1).

Lemma 4.1

Let $f: \mathbb R\times X \rightarrow \mathbb R$ be a $C^1$ function satisfying the $({\text {PS}})_{I,a}$ condition for a given $a\in \mathbb R$ which is a regular value for every $f_\lambda $, with $\lambda \in I$. Then, there exist $\varepsilon , \delta > 0$ such that $\Vert f_\lambda '(x)\Vert \ge \varepsilon $ for every $(\lambda , x) \in f_{I}^{-1}((a - \delta , a + \delta ) )$.

Proof

Assume by contradiction that there exists a sequence $(\lambda _n, x_n) \in I \times X$ such that $\Vert f_{\lambda _n}'(x_n)\Vert \rightarrow 0$ and $f(\lambda _n,x_n) \rightarrow a$. Taking a convergent subsequence $(\lambda _{n_j})$ and a convergent subsequence $(x_{n_j})$ given by the $({\text {PS}})_{I,a}$ condition, we deduce that a is a singular value. $\square $

Lemma 4.2

Consider a closed set $J \subset \mathbb R$ and let $f: \mathbb R\times X \rightarrow \mathbb R$ be a $C^1$ function satisfying the $({\text {PS}})_{I,J}$ condition. Then the set

$$\begin{aligned} K = \{(\lambda , c) \in I \times J : \exists x \in X, f_\lambda (x) = c, f_\lambda '(x) = 0\} \end{aligned}$$

is closed.

Proof

Take a convergent sequence $(\lambda _n, c_n) \rightarrow (\lambda , c) \in I \times J, \ (\lambda _n, c_n) \in K$, and consider $x_n \in X$, for any n, such that $f(\lambda _n, x_n) = c_n$, $f_\lambda '(x_n) = 0$. By the $({\text {PS}})_{I,c}$ condition there exists a convergent subsequence of $(x_n)$. Thus, the continuity of $f_\lambda '$ shows that $(\lambda , c) \in K$. $\square $

Lemma 4.3

Let $f: \mathbb R\times X \rightarrow \mathbb R$ be a $C^1$ function satisfying $({\text {PS}})_{I,\{a,b\}}$ where $a<b$ are regular values of $f_\lambda $ for $\lambda \in I$. Denote $U_t = (a-t, a+t) \cup (b-t, b+t)$. Assume that $\partial _1 f$ is bounded in $f_{I }^{-1}(U_\delta )$ for some $\delta > 0$. Then, there exists a function $v: \mathbb R\times X \rightarrow X$ such that

(i)
v is bounded and locally Lipschitz.
(ii)
$\partial _1 f(\lambda , x) + f_\lambda '(x)[v(\lambda , x)] < 0$ if $\lambda \in I$ and $f_\lambda (x) = a \hbox { or } b$.

Remark 4.4

The reader can understand the notation $f_{I }^{-1}(U_\delta )$ by the analogous one in the statement of Theorem 3.3.

Proof

First, by Lemma 4.1 we may assume, taking a smaller $\delta >0$ if necessary, that, for some $\varepsilon >0$, $\Vert f_\lambda '(x)\Vert \ge \varepsilon $ for all $(\lambda , x) \in f_{I }^{-1}(U_\delta )$. Let $\nu :\mathbb R\rightarrow [0,1]$ be a continuous function equal to 0 in $U_{\delta /2}$ and equal to 1 in $\mathbb R\setminus U_{\delta }$. We shall construct $v(\lambda , x)$ satisfying the inequality

$$\begin{aligned} \partial _1 f(\lambda , x) + f_\lambda '(x)[v(\lambda , x)] <\nu (f_\lambda (x))\left( |\partial _1 f(\lambda , x)| +1 \right) . \end{aligned}$$

(4.1)

Thus, condition (ii) will follow. To this purpose, fix $(\lambda , x) \in I \times X$ and assume $f_\lambda (x) \in U_\delta $, so that $\Vert f_\lambda '(x)\Vert \ge \varepsilon $. There exists $w_{\lambda , x}\in X$ such that

$$\begin{aligned} \Vert w_{\lambda , x}\Vert \le \frac{2}{\varepsilon }\left( |\partial _1 f(\lambda , x)| + 1\right) \end{aligned}$$

and

$$\begin{aligned} f_\lambda '(x)[w_{\lambda , x}] \le -(|\partial _1 f(\lambda , x)| + 1). \end{aligned}$$

Hence, we have $\partial _1 f(\lambda , x) + f_\lambda '(x)[w_{\lambda , x}] < 0$. On the other hand, if $f_\lambda (x) \not \in U_\delta $, we define $w_{\lambda , x} = 0$. In both cases, we obtain

$$\begin{aligned} \partial _1 f(\lambda , x) + f_\lambda '(x)[w_{\lambda , x}] <\nu (f_\lambda (x))\left( |\partial _1 f(\lambda , x)| +1 \right) . \end{aligned}$$

By continuity, every $(\lambda , x) \in I \times X$ has a neighborhood $V^{\lambda , x}$ in $\mathbb R\times X$ such that

$$\begin{aligned} \partial _1 f(\alpha , y) + f_\alpha '(y)[w_{\lambda , x}] <\nu (f_\alpha (y))\left( |\partial _1 f(\alpha , y)| +1 \right) \end{aligned}$$

(4.2)

for every $(\alpha , y) \in V^{\lambda , x}$. Since $I \times X$ is paracompact and $\{V^{\lambda , x} \}_{\lambda , x}$ is an open covering of $I \times X$, we obtain a countable, locally finite refinement $V_i \subseteq V^{\lambda _i, x_i}$ covering $I \times X$, and a locally Lipschitz partition of unity, that is, a collection of (locally Lipschitz) nonnegative functions $\eta _i:\mathbb R\times X \rightarrow \mathbb R$ with support in $V_i$ and such that

$$\begin{aligned} \sum _{i\in \mathbb N} \eta _i (\lambda ,x)= 1 \quad \quad \forall (\lambda ,x)\in I \times X, \end{aligned}$$

where the above sum is locally finite. Recalling (4.2), we have, for any i and any $(\alpha , y)\in I \times X$,

$$\begin{aligned} \eta _i(\alpha , y) \partial _1 f(\alpha , y) + f_\alpha '(y)[\eta _i(\alpha , y) w_{\lambda , x}] \le \eta _i(\alpha , y) \nu (f_\alpha (y))\left( |\partial _1 f(\alpha , y)| +1 \right) , \end{aligned}$$

with the strict inequality if $\eta _i(\alpha , y) > 0$. Then, we obtain

$$\begin{aligned} \sum _{i \in \mathbb N} \eta _i(\alpha , y) \left( \partial _1 f(\alpha , y) + f_\alpha '(y)[w_{\lambda , x}] \right) < \sum _{i \in \mathbb N} \eta _i(\alpha , y) \nu (f_\alpha (y))\left( |\partial _1 f(\alpha , y)| +1 \right) . \end{aligned}$$

Now, define

$$\begin{aligned} v(\lambda , x) =\sum _{i \in \mathbb N} \eta _i(\lambda , x) w_{\lambda _i, x_i}. \end{aligned}$$

We have

$$\begin{aligned} \partial _1 f(\alpha , y) + f_\alpha '(y)[v(\lambda , x)] <\nu (f_\alpha (y))\left( |\partial _1 f(\alpha , y)| +1 \right) . \end{aligned}$$

Since $\Vert w_{\lambda , x}\Vert \le \frac{2}{\varepsilon }\left( |\partial _1 f(\lambda , x)| + 1\right) $ for every $(\lambda , x) \in I \times X$, we have, for any $(\alpha , y) \in \mathbb R\times X$,

$$\begin{aligned} \Vert v(\alpha , y)\Vert \le \sum _{i \in \mathbb N} \eta _i(\alpha , y) \Vert w_{\lambda _i, x_i} \Vert \le \frac{2}{\varepsilon }\left( \sup _{(\lambda , x) \in f_{I }^{-1}(U_\delta )} |\partial _1 f(\lambda , x)| + 1 \right) \end{aligned}$$

and v is bounded. Finally, it is immediate to observe that v is locally Lipschitz and this concludes the proof. $\square $

The next two theorems are key to the study of deformation of one-parameter families of functions. Theorems 4.5 and 4.6 generalize analogous results in the textbook [9], where they appear under much stronger conditions.

Theorem 4.5

(Deformation Theorem). Let $f: \mathbb R\times X \rightarrow \mathbb R$ be $C^1$ and $a<b$ regular values of $f_\lambda $ for $\lambda \in I$. Assume that f satisfies $({\text {PS}})_{I,\{a,b\}}$ and that $\partial _1 f$ is bounded in $f_{I }^{-1}(U_\delta )$ for some $\delta > 0$. Then the pairs $\left( f_{-1}^{(b)} , f_{-1}^{(a)} \right) $ and $\left( f_1^{(b)} , f_1^{(a)} \right) $ are homotopy equivalent.

Proof

The vector field v constructed in Lemma 4.3 is locally Lipschitz and bounded, so it generates a globally defined flow

$$\begin{aligned} \phi : \mathbb R\times \mathbb R\times X \rightarrow X, \end{aligned}$$

which satisfies

$$\begin{aligned} \frac{\partial }{\partial t} \phi (t, \lambda , x) = v(t+\lambda , \phi (t, \lambda , x)). \end{aligned}$$

For $(\lambda _0, x_0) \in I \times X$, the curve $x(t) = \phi (t, \lambda _0, x_0)$ is the solution of the initial value problem

$$\begin{aligned} \left\{ \begin{array}{l} x'(t) = v(\lambda _0 + t,x(t))\\ x(\lambda _0) = x_0. \end{array}\right. \end{aligned}$$

(4.3)

For any $(\lambda , x) \in \mathbb R\times X$ define $\varphi (t) = f_{t+\lambda }(\phi (t, \lambda , x))$, which verifies

$$\begin{aligned} \varphi '(t) = \partial _1 f(t+\lambda , \phi (t, \lambda , x)) + f_{t+\lambda }'(\phi (t, \lambda , x))[v(t+\lambda , \phi (t, \lambda , x)]. \end{aligned}$$

Notice that, by condition (ii) of Lemma 4.3, $\varphi (t) = a$ implies $\varphi '(t) < 0$. So, if $\varphi (0) \le a$, then we have $\varphi (t) < a$ for every $t>0$. If $x \in f_\lambda ^{(a)} $, then, by the definition of $\varphi $ and the previous consideration, $\phi (t, \lambda , x) \in f_{t+\lambda }^{(a)} $. We can write it as

$$\begin{aligned} \phi \left( t,\lambda ,f_\lambda ^{(a)} \right) \subseteq f_{t+\lambda }^{(a)} . \end{aligned}$$

Similarly, for b we obtain

$$\begin{aligned} \phi \left( t,\lambda ,f_\lambda ^{(b)} \right) \subseteq f_{t+\lambda }^{(b)} . \end{aligned}$$

Applying the same reasoning to the function $\bar{f}(\lambda , x) := f(-\lambda , x)$, we obtain a (globally defined) flow $\bar{\phi }: \mathbb R\times \mathbb R\times X \rightarrow X$ such that

$$\begin{aligned} \bar{\phi }\left( t,\lambda ,\bar{f}_\lambda ^{(a)} \right) \subseteq \bar{f}_{t+\lambda }^{(a)} ,\ \ \bar{\phi }\left( t,\lambda ,\bar{f}_\lambda ^{(b)} \right) \subseteq \bar{f}_{t+\lambda }^{(b)} \end{aligned}$$

for every $t>0$.

The functions $F(x) = \phi (2,-1,x)$, $G(x) = \bar{\phi }(2,-1,x)$ can be seen, with an abuse of notation (see Preliminaries), as continuous functions of pairs

$$\begin{aligned} F:\left( f_{-1}^{(b)} , f_{-1}^{(a)} \right) \rightarrow&\left( f_1^{(b)} , f_1^{(a)} \right) \\ G:\left( f_1^{(b)} , f_1^{(a)} \right) \rightarrow&\left( f_{-1}^{(b)} , f_{-1}^{(a)} \right) . \end{aligned}$$

Define

$$\begin{aligned} H_t(x) = \bar{\phi }(t,1-t,\phi (t,-1,x)),\ \ \bar{H}_t(x) = \phi (t,1-t,\bar{\phi }(t,-1,x)). \end{aligned}$$

Then, we verify that $H_t$, $\bar{H}_t$ are functions of pairs

$$\begin{aligned} H_t:\left( f_{-1}^{(b)} , f_{-1}^{(a)} \right) \rightarrow \left( f_{-1}^{(b)} , f_{-1}^{(a)} \right) ,\ \ \bar{H}_t:\left( f_1^{(b)} , f_1^{(a)} \right) \rightarrow \left( f_1^{(b)} , f_1^{(a)} \right) \end{aligned}$$

for $t>0$. In addition, $H_0(x) = x, H_2(x) = G(F(x)), \bar{H}_0(x) = x, \bar{H}_2(x) = F(G(x))$. Thus, F and G are homotopy equivalences. $\square $

Theorem 4.6

Let (r,s) be an open bounded interval and let $a,b:I \rightarrow (r,s)$ be two continuous functions such that $a(\lambda ) < b(\lambda )$ for any $\lambda $, and $f: \mathbb R\times X \rightarrow \mathbb R$ a $C^1$ function satisfying the $({\text {PS}})_{I,[r,s]}$-condition.

Assume that $\partial _1 f: I \times X \rightarrow \mathbb R$ is bounded in the set $f_{I }^{-1}(r, s)$. Assume also that $a(\lambda ), b(\lambda )$ are regular values of $f_\lambda $ for every $\lambda \in I$. Then the pairs $\left( f_{-1}^{(b({-1}))} , f_{-1}^{(a({-1}))} \right) $ and $\left( f_1^{(b(1))} , f_1^{(a(1))} \right) $ are homotopy equivalent.

Proof

By hypothesis, the graphs of a,b in $I \times \mathbb R$ do not intersect the set

$$\begin{aligned} K = \{(\lambda , c) \in I \times [r,s]: \; \exists x \in X, f_\lambda (x) = c, f_\lambda '(x) = 0\}. \end{aligned}$$

Since K is closed by Lemma 4.2, the graphs of the functions a,b can be approximated by $C^1$ functions with the same endpoints $a(\pm 1)$ and $b(\pm 1)$. Thus we may assume a,b are $C^1$. We consider the function

$$\begin{aligned} g(\lambda , x) = \frac{ f(\lambda , x) - a(\lambda )}{b(\lambda ) - a(\lambda )}. \end{aligned}$$

Thus, g satisfies

$$\begin{aligned} f_\lambda ^{(a(\lambda ))} = g_\lambda ^{(0)} ,\quad \quad f_\lambda ^{(b(\lambda ))} = g_\lambda ^{(1)} , \end{aligned}$$

and it is easy to check that g verifies the conditions of Theorem 4.5 with $a=0, b=1$. $\square $

Proofs of Theorems 3.3 and 3.4

First, we prove two technical lemmas.

Lemma 5.1

Let $D \subset \mathbb R^2$ be a closed rectangle, $A_0, A_1$ be two opposite sides of D and $B_0, B_1$ be the other two. Let $S \subset D$ be a compact set. If S does not contain a connected component intersecting $B_0$ and $B_1$, then there exists a continuous curve $\gamma :[0,1] \rightarrow D$ with $\gamma (0) \in A_0$ and $\gamma (1) \in A_1$ and not intersecting S, $B_0$ and $B_1$.

Proof

Without loss of generality, we can assume that $A_0, A_1$ are vertical sides and $B_0, B_1$ horizontal. Let $S_i = S \cap B_i, i = 0,1$ and assume there is no connected component of S which intersects $S_0$ and $S_1$ at the same time. We may assume that $S_i \ne \emptyset $ because, otherwise, a horizontal line close to $B_i$ would be the desired curve. By Whyburn's lemma there is a separation $S = C_0 \cup C_1$ where $S_i \subseteq C_i$ and $C_0, C_1$ are two nonempty disjoint compact sets. The sets $C_i \cup B_i$ are also nonempty disjoint and compact. By the smooth Urysohn lemma [29, corollary of Theorem 1.11] there exists a $C^\infty $ smooth function $g: \mathbb R^2 \rightarrow \mathbb R$ such that $g(x) = i$ for all $x \in C_i \cup B_i, i = 0,1$.

Take $\alpha \in (0,1)$ a regular value of the three functions $g, g|_{A_0}, g|_{A_1}$ and consider

$$\begin{aligned} L = g^{-1}(\alpha ) \cap \left( D \setminus (B_0 \cup B_1)\right) \end{aligned}$$

which is a one-dimensional differentiable manifold with boundary, with $\partial L = L \cap (A_0 \cup A_1)$ and $L \cap S = \emptyset $. Since $g(x) = i$ for all $x \in B_i$, $i=0,1$, and $\alpha $ is a regular value of $g|_{A_i}, i=0,1$, then the cardinality of $L \cap A_i$ is odd, for $i=0,1$. Therefore, there is a curve of L having one endpoint in each of the $A_i$'s. $\square $

Lemma 5.2

Let $a, b :[-1,1] \rightarrow [-1,1]$ be two continuous functions satisfying

$$\begin{aligned} a(-1)=b(-1)=-1, \quad \quad a(1)=b(1)=1. \end{aligned}$$

Then for every $\varepsilon > 0$ there exist continuous functions $\tilde{a}, \tilde{b}, c, d:[-1,1] \rightarrow [-1,1]$ such that

1.
$\tilde{a}(-1)=\tilde{b}(-1)=-1$,$\tilde{a}(1)=\tilde{b}(1)=1$,
2.
$c(-1)=d(-1)=-1$,$c(1)=d(1)=1$,
3.
$\Vert \tilde{a} - a\Vert _\infty< \varepsilon , \quad \Vert \tilde{b} - b\Vert _\infty < \varepsilon $,
4.
$\tilde{a}(c(t)) = \tilde{b}(d(t))$.

Proof

We approximate a,b by smooth functions $\tilde{a}, \tilde{b} :[-1,1] \rightarrow [-1,1]$ satisfying conditions 1, 3 above and

(i)
$\tilde{a}'(-1), \tilde{b}'(-1), \tilde{a}'(1), \tilde{b}'(1) > 0$,
(ii)
the critical values of $\tilde{a}$ and $\tilde{b}$ are disjoint,
(iii)
$\tilde{a}(x), \tilde{b}(x) \in (-1,1)$ for all $x \in (-1,1)$.

Let $D = [-1,1] \times [-1,1]$ and $\phi :D \rightarrow \mathbb R$, defined as $\phi (x,y) = \tilde{a}(x) - \tilde{b}(y)$. Condition (ii) guarantees that 0 is a regular value of $\phi |_{D^0}$, where $D^{0}$ stands for the interior of D. Let $L = \phi ^{-1}(0)$. Since condition (iii) implies

$$\begin{aligned} \begin{array}{ll} \phi (1,t)>0, &{} \quad \phi (t,-1) >0,\\ \phi (-1,t)<0, &{} \quad \phi (t,1) < 0, \end{array} \end{aligned}$$

for all $t \in (-1,1)$, we have $L \cap \partial D= \{(-1,-1), (1,1)\}$. Even if D is not a manifold with boundary (because of the vertices) by condition (i), L can be parameterized near $(-1,-1)$ and (1, 1) with curves entering $D^0$. Thus, L is a differentiable manifold of dimension 1 with boundary $\{(-1,-1), (1,1)\}$ which must connect these two points. Parameterize the curve inside L connecting $(-1,-1)$ and (1, 1) by (c(t),d(t)). Then c,d satisfy

$$\begin{aligned} 0 = \phi (c(t), d(t)) = \tilde{a}(c(t)) - \tilde{b}(d(t)). \end{aligned}$$

$\square $

Proof of Theorem 3.3

Let $\varepsilon > 0$ be small enough so that the two disks $B_{-1} = B((-1,0), \varepsilon )$ and $B_1 = B((1,0), \varepsilon )$ contain only trivial critical pairs.

Let $G_f$ be the connected component of $E_f \cup Z_{{\text {in}}}$ containing $Z_{{\text {in}}}$ [recall formulas (3.2) and (3.3) for the definitions of $E_f$ and $Z_{{\text {in}}}$]. Assume by contradiction that none of alternatives 1 and 2 in the statement of the theorem, are satisfied for $G_f$. Then, there is $R>0$ such that $G_f \subseteq [-1,1] \times [-R,R]$.

The set $D_+ = [-1,1] \times [0,R]$ is homeomorphic to a closed rectangle, where the vertical sides correspond to $\{-1, 1\} \times [0,\varepsilon ]$ and the horizontal lines to the rest of $\partial D_+$, this is $Z_{{\text {in}}}$ and the three segments

$$\begin{aligned} S_{{\text {out}}}:= ( \{-1,1\} \times [\varepsilon ,R] ) \cup ( [-1,1] \times \{R\} ). \end{aligned}$$

The reader can see the above Fig. 1. If claim 2 of the theses of the theorem fails, then there is no connected set inside $E_f$ that intersects at the same time both horizontal sides of the rectangle. Therefore, applying Lemma 5.1 which is invariant by homeomorphisms, as it is easy to see, we conclude that there exists a continuous curve

$$\begin{aligned} u_+:[-1,1] \rightarrow D_+ \setminus E_f \end{aligned}$$

such that

$$\begin{aligned} u_+(-1) = (-1,\varepsilon /2), \quad u_+(1) = (1,\varepsilon /2). \end{aligned}$$

Similarly, define $D_-$ in the lower semiplane and a map

$$\begin{aligned} u_-:[-1,1] \rightarrow D_- \setminus E_f \end{aligned}$$

such that

$$\begin{aligned} u_-(-1) = (-1,-\varepsilon /2), \quad u_-(1) = (1,-\varepsilon /2), \end{aligned}$$

and having analogous properties to $u_{+}.$ Denote

$$\begin{aligned} u_{+}(t)=(\lambda _{+}(t),y_{+}(t)), \quad u_{-}(t)=(\lambda _{-}(t),y_{-}(t)). \end{aligned}$$

By Lemma 5.2 with $\varepsilon < {\text {dist}}(S_f, {\text {Im}}(u_\pm ))$ and a,b replaced by $\lambda _- , \lambda _+$, we obtain functions $\tilde{\lambda }_-, \tilde{\lambda }_+, c, d:[-1,1] \rightarrow [-1,1]$ such that

1.
$\tilde{u}_\pm (t): = (\tilde{\lambda }_\pm (t), y_\pm (t) ) \in \mathbb R^2 \setminus S_f$ for all $t \in [-1,1]$,
2.
$\tilde{\lambda }_-(c(t)) = \tilde{\lambda }_+(d(t))$.

Now define

$$\begin{aligned} \lambda (t)&= \tilde{\lambda }_-(c(t)) = \tilde{\lambda }_+(d(t)),\\ a(t)&= y_-(c(t)),\\ b(t)&= y_+(d(t)). \end{aligned}$$

By the properties of the curves $\tilde{u}_\pm $ we know that a(t) and b(t) are regular values of $f_{\lambda (t)}:X\rightarrow \mathbb R$, for any $t\in [0,1]$. Applying Theorem 4.6 to the family of maps $f_{\lambda (t)}$, we get the homotopy equivalence of pairs

$$\begin{aligned} \left( f_{-1}^{(b({-1}))} , f_{-1}^{(a({-1}))} \right) \cong \left( f_1^{(b(1))} , f_1^{(a(1))} \right) . \end{aligned}$$

In view of assumption (iii), we have

$$\begin{aligned} \left( f_{-1}^{(\delta )} , f_{-1}^{(-\delta )} \right) \cong \left( f_1^{(\delta )} , f_1^{(-\delta )} \right) \end{aligned}$$

for any $\delta \in (0, \varepsilon /2)$, which contradicts hypothesis (iv). $\square $

Proof of Theorem 3.4

We want to prove that conditions 3.4(iii) and 3.4(iv) imply conditions 3.4(iii) and 3.4(iv). [Actually conditions 3.4(i) and 3.4(ii) coincide with 3.4(i) and 3.4(ii).] Here, the reader could notice that we have used a simplified notation to refer to the assumptions of Theorems 3.3 and 3.4.

The facts that f is $C^2$ and that $0 \in H$ is a nondegenerate critical point [condition 3.4(iii)] imply 3.4(iii).

It remains to show that conditions 3.4(iii) and 3.4(iv) imply condition 3.4(iv). Assume the pairs of spaces $\left( f_{-1}^{(\delta )} , f_{-1}^{(-\delta )} \right) $ and $\left( f_1^{(\delta )} , f_1^{(-\delta )} \right) $ are homotopy equivalent for $\delta >0$ arbitrarily small. Then, by Theorem 2.2 and the fact that $0 \in H$ is the only critical point with value 0 [condition 3.4(iii)], we can compute the critical groups for every $k \in \mathbb N$ as

$$\begin{aligned} C_k(f_i, 0) \cong H_k\left( f_i^{(\varepsilon /2)} , f_i^{(-\varepsilon /2)} \right) \end{aligned}$$

for $i = -1,1$.

The remainder of the proof is standard. Condition 3.4(iv) permits to reduce the computation of the critical groups to finite-dimensional spaces, and the condition

$$\begin{aligned} \mu (L_{-1}) \ne \mu (L_1) \end{aligned}$$

implies that $C_k(f_{-1}, 0)$ is not isomorphic to $C_k(f_{1}, 0)$ for some k, which is a contradiction. $\square $

Strongly indefinite functions

In this section we will prove a global bifurcation result for a class of nonlinear functionals verifying analogous conditions of Theorem 3.4, except for the fact that the Hessian operators of the functionals have here infinite-dimensional negative eigenspaces and thus the Morse index cannot be defined. Condition (iv) of Theorem 3.4 will be replaced in Theorem 6.1 by a more general one involving the spectral flow of the Hessian operators. On the other hand, Theorem 6.1 is not strictly considered as an extension of Theorem 3.4 because it requires a special compactness assumption, as we will see below. With a slight abuse of notation, in the sequel $\nabla f(\lambda ,x)$ will denote the Fréchet derivative of f with respect to the second variable.

Theorem 6.1

Let $f : \mathbb R\times H \rightarrow \mathbb R$ be a $C^2$ function such that

$$\begin{aligned} f(\lambda ,0) = 0\quad \text {and} \quad \nabla f(\lambda ,0) = 0, \quad \quad \forall \lambda \in \mathbb R. \end{aligned}$$

Suppose that, for every $(\lambda ,x) \in \mathbb R\times H$, one has $\nabla f(\lambda ,x) = \mathcal {J}(x) - K(\lambda , x)$ where $\mathcal {J}$ a symmetry of H and the range of $K:\mathbb R\times H \rightarrow H$ is contained in a compact set. Denote by I the interval $ [-1,1]$ and assume that the following assumptions hold:

(i)
f satisfies the $({\text {PS}})_{\mathbb R,\mathbb R}$ condition.
(ii)
$\partial _1 f$ is bounded in the sets of the form $f_{[-N, N]}^{-1}([-N, N])$ for every $N \in \mathbb N$.
(iii)
For $i = -1,1$, $0 \in H$ is a nondegenerate critical point and the only critical point of $f_i$ with value 0.
(iv)
Assume that, for every $\lambda \in I$, the Hessian of f with respect to the second variable at $x=0$,

$$\begin{aligned} L_\lambda := \partial _2 \nabla f(\lambda , 0), \end{aligned}$$

is Fredholm for every $\lambda \in [-1,1]$ and suppose

$$\begin{aligned} {\text {sf}}(L,I)\ne 0. \end{aligned}$$

Then the conclusion of Theorem 3.3 holds.

Recalling Sect. 2, let $H=H_{+}\oplus H_{-}$ be the orthogonal splitting produced by $\mathcal {J}$ and let $\{e_{n}^{{\pm }}, \; n\in \mathbb N\}$ be two Hilbert bases of $H_{+}$ and $H_{-}$, respectively. Call $H_{n}$ the 2n-dimensional subspace of H generated by $\{e_{k}^{{\pm }}, \; k\le n\}$. As in Sect. 2, denote by $P_{n}:H\rightarrow H_{n}$ the orthogonal projection and define $f_n$ as the restriction of $P_{n}f$ to $\mathbb R\times H_n$. Clearly we have

$$\begin{aligned} \nabla f(\lambda ,x)&= \mathcal {J}(x) - K(\lambda ,x),\\ \nabla f_n(\lambda ,x)&= \mathcal {J}(x) - K_n(\lambda ,x),\\ \partial _{2} \nabla f_n(\lambda ,x)&= \mathcal {J}- \partial _{2}K_n(\lambda ,x), \end{aligned}$$

where $K_n(\lambda ,x) = P_n K(\lambda ,x)$. We need three technical lemmas.

Lemma 6.2

There are $\varepsilon >0$ and $m_0 \in \mathbb N$ such that, for $m \ge m_0$, the balls $B((\pm 1,0),\varepsilon ) \subseteq \mathbb R^2$ contain only trivial critical pairs of $f_m$.

Proof

Assume the contrary. Then, we have a sequence $(\lambda _n,x_n) \in \mathbb R\times H$ such that

$$\begin{aligned}&x_n \in H_n\setminus H_{n-1}\\&\lambda _n \rightarrow \lambda ^* = \pm 1\\&f(\lambda _n, x_n) \rightarrow 0\\&\nabla f(\lambda _n, x_n) = 0. \end{aligned}$$

Since $\mathcal {J}(H_n) = H_n$ and $P_n \rightarrow Id$ uniformly in compact sets, and since K has compact image, we have a subsequence, we still call $(x_{n})$, such that

$$\begin{aligned} x_n = \mathcal {J}P_n K(\lambda _n, x_n) \rightarrow x^*. \end{aligned}$$

(In the above equality, we also use the fact that the inverse of $\mathcal {J}$ is $\mathcal {J}$.) By the continuity of f and $\nabla f$,

$$\begin{aligned} f(\lambda ^*, x^*) = 0, \quad \nabla f(\lambda ^*, x^*) = 0. \end{aligned}$$

By the assumption (iii), we have $x^* = 0$. Now, since f is $C^2$, we have

$$\begin{aligned} 0= & {} \nabla f_n(\lambda _n, x_n) = \partial _{2} \nabla f_n(\lambda ^*, 0)\, x_n + o(\Vert x_n\Vert )\\ 0= & {} \partial _{2}\nabla f(\lambda ^*, 0)\, x_n + (Id - P_n)\, \partial _{2} K(\lambda ^*, 0)\, x_n + o(\Vert x_n\Vert ). \end{aligned}$$

Since the Frechet derivative of a compact function is a compact operator [20, Theorem 17.1], and since $P_n \rightarrow Id$ uniformly in compact sets, we have (modulo a subsequence)

$$\begin{aligned} \Vert (Id - P_n)\, \partial _{2} K(\lambda ^*, 0)\, x_n\Vert = o(\Vert x_n\Vert ). \end{aligned}$$

Hence, we conclude that ${\partial _{2} \nabla f(\lambda ^*,0)\, x_n} = o(\Vert x_n\Vert )$ which contradicts the invertibility of $\partial _{2} \nabla f(\lambda ^*,0)$. The lemma is thus proven. $\square $

The following lemma can be easily verified.

Lemma 6.3

For any m, the function $f_m$ satisfies $(PS)_{\mathbb R,\mathbb R}$.

Proof

Assume there is a sequence $(\lambda _n, x_n) \in \mathbb R\times H_m$ such that

$$\begin{aligned}&f_m(\lambda _n, x_n) \rightarrow c \\&\nabla f_m(\lambda _n, x_n) = \mathcal {J}(x_n) - K_m(\lambda _n, x_n) \rightarrow 0. \end{aligned}$$

Then, by the compactness of $K_m$, there is a subsequence, again called ($x_n$), such that $\mathcal {J}K_m(\lambda _n, x_n)$ converges, and thus

$$\begin{aligned} x_n = \mathcal {J}(\nabla f_m(\lambda _n, x_n)) + \mathcal {J}K_m(\lambda _n, x_n) \end{aligned}$$

also converges. $\square $

Also we prove the following result.

Lemma 6.4

If $(z_n) \subset \mathbb R^2$ is a convergent sequence such that $z_n \in S_{f_n}$, then $z = \lim z_n \in S_f$.

Proof

Take $(\lambda _n, x_n) \in \mathbb R\times H_n$ such that $(\lambda _n, f(t_n, x_n)) = z_n$ and $\nabla f_n(\lambda _n, x_n) = 0$. We have

$$\begin{aligned} x_n = \mathcal {J}K_n(\lambda _n, x_n). \end{aligned}$$

Thus, taking a subsequence of $\mathcal {J}K_n(\lambda _n, x_n)$, we have

$$\begin{aligned} x = \lim _{n \rightarrow \infty } x_n = \mathcal {J}K(\lambda , x) \end{aligned}$$

and $(\lambda , f(\lambda , x)) = z$. $\square $

For sufficiently large m, the spectral flow of the Hessian operators of f, ${\text {sf}}(L,I)$, which is nonzero according to the assumptions of Theorem 6.1, is computed as $\mu (L_{m,-1}) - \mu (L_{m,1})$, where $\mu (L_{m,\lambda })$ is the Morse index of the Hessian of $f_{m}(\lambda ,\cdot )$. Therefore, considering Lemma 6.3, the function $f_m$ is in the hypotheses of Theorem 3.4. We obtain for every $m \ge m_0$ a family of closed connected sets $C_m \subseteq S_{f_m}$ satisfying the conclusion of Theorem 3.3. Now we can prove the main result of this section.

Proof of Theorem 6.1

As in the proof of Theorem 3.3, assume none of the alternatives 1 and 2 are satisfied. Take $G_f \subseteq \mathbb R^2, R>0, D_+,D_-$ and $S_{{\text {out}}}$ as in the proof of Theorem 3.3, and $\varepsilon > 0$ as in Lemma 6.2. The set $G_f$ is contained in $D_+$, contains $Z_{in}$ and does not intersect $S_{{\text {out}}}$. Again by Whyburn's lemma, there exists an open set A containing $G_f$ and such that

$\overline{A} \in D_+$,
$\partial A \cap (E_f \cup S_{{\text {out}}}) = \emptyset $.

For every $m > m_0$ we have nonempty intersections $z_m \in C_m \cap \partial A$. By Lemma 6.2, we have $z_m \not \in B_{\pm 1}$. Taking a convergent subsequence given by the compactness of $\partial A$, we may assume $z_m \rightarrow z$ with $z \in \partial A$. Finally, by Lemma 6.4 we obtain $z \in S_f$. Since $z \not \in Z_{{\text {in}}}\cup S_{{\text {out}}}$ we deduce $z \in E_f$, which is a contradiction. $\square $

Example of application in a second-order ODE

In order to show the applicability of our method, we consider the following parameterized second-order differential equation with periodic boundary conditions:

$$\begin{aligned} \left\{ \begin{array}{l} x''(t) = -g'(x(t)) p_\lambda (t) \\ x(0) = x(2 \pi )\\ x'(0) = x'(2 \pi ). \end{array}\right. \end{aligned}$$

(7.1)

where we assume that

(i)
the map $g: \mathbb R\rightarrow \mathbb R$ is $C^2$ with $g(0) = g'(0) = 0$;
(ii)
the limits $\lim _{s \rightarrow - \infty }g'(s)< 0 < \lim _{s \rightarrow +\infty }g'(s)$ exist and are finite;
(iii)
the real map $p(\lambda ,t)=p_{\lambda }(t)$ is continuous and bounded on $[-1,1]\times \mathbb R$;
(iv)
any $p_{\lambda }$ is $2\pi $-periodic;
(v)
$p_{-1}$ and $p_{1}$ are constant;
(vi)
$\int _0^{2\pi } p_{\lambda }(t) \hbox {d}t \ne 0$ for every $\lambda \in [-1,1]$.

Call $H = H^1_{per}([0,2\pi ], \mathbb R)$ the subspace of the Hilbert space $H^1([0,2\pi ],\mathbb R)$ consisting of $2 \pi $-periodic absolutely continuous functions with derivative in $L^2$. Then define the action functional

$$\begin{aligned}&f:[-1,1] \times H \rightarrow \mathbb R\\&f_\lambda (x) = \frac{1}{2} \int _0^{2\pi } x'(t)^2 \hbox {d}t - \int _0^{2\pi } g(x(t)) p_\lambda (t) \hbox {d}t.\\ \end{aligned}$$

Compute the derivatives

$$\begin{aligned} f'_\lambda (x)[v]&= \int _0^{2\pi } x'(t) v'(t) \hbox {d}t - \int _0^{2\pi } g'(x(t)) p_\lambda (t) v(t) \hbox {d}t\\ f''_\lambda (0)[v,w]&= \int _0^{2\pi } v'(t) w'(t) \hbox {d}t - c \int _0^{2\pi } p_\lambda (t) v(t)w(t) \hbox {d}t \end{aligned}$$

so that $x \in H$ is a (classic) solution of (7.1) if and only if $f'(x) = 0$. Let us show that f satisfies the hypotheses of Theorem 3.4 for some values of $a_{\pm 1}$ and c, where we denote $p_{-1}(t) = a_{-1}$, $p_{1}(t) = a_1$ and $g''(0)=c$. For convenience denote $\kappa _i = \sqrt{a_i c}$.

First of all, the fact that f is $C^2$ and satisfies the $({\text {PS}})_{\mathbb R,\mathbb R}$ condition can be verified thanks to the smoothness and growth condition of g. The proof is standard but rather technical, and we only describe the main lines. We follow the proof of [2, Lemma 3.1].

Assume that

$$\begin{aligned} |f_{\lambda _n}(y_n)| \rightarrow c, \quad \Vert f'_{\lambda _n}(y_n)\Vert _{H^*} := \varepsilon _n\rightarrow 0, \quad \lambda _n \rightarrow \lambda \end{aligned}$$

(7.2)

where $H^*$ denotes the dual space of H. We claim that $y_n$ is bounded: indeed, otherwise we may suppose that $\Vert y_n\Vert _H \rightarrow \infty $. Set $v_n = \frac{y_n}{\Vert y_n\Vert _H }$, then taking a subsequence we may assume that $v_n\rightarrow v$ weakly and $v_n\rightarrow v$ uniformly. Moreover, from the inequality

$$\begin{aligned} \frac{1}{2} \int _0^{2\pi } y_n'(t)^2 \hbox {d}t - \int _0^{2\pi } g(y_n(t)) p_{\lambda _n}(t) \hbox {d}t \le C \end{aligned}$$

and $|g(u)| \le C|u|$ we obtain

$$\begin{aligned} \int _0^{2\pi } \frac{y_n'(t)^2}{\Vert y_n\Vert _H^2}\; \hbox {d}t \rightarrow 0. \end{aligned}$$

We also have that

$$\begin{aligned} \Vert y_n - y_n(0)\Vert _\infty \le C\Vert y_n'\Vert _{L^2} \end{aligned}$$

for some constant C. Thus, if we write

$$\begin{aligned} v_n = \frac{y_n-y_n(0)}{\Vert y_n\Vert _H} +\frac{y_n(0)}{\Vert y_n\Vert _H}, \end{aligned}$$

the first term goes to 0. Then, taking a subsequence we may assume that $v_n \rightarrow c_0$ uniformly for some constant $c_0\ne 0$. Furthermore, $v_n \rightarrow 0$ in $L^2$ and we conclude that $v_n \rightarrow c_0$ in H. This means that $y_n$ diverges either to $+\infty $ or $-\infty $. Then the limit condition of $g'$ can be exploited as in [2, Lemma 3.1] to conclude that $f'_{\lambda _n}(y_n)[v_n]$ cannot converge to 0 and this is a contradiction.

Now that $y_n$ is bounded in H, taking a subsequence we may assume that $y_n\rightarrow y$ weakly in $H^1$ and uniformly for some y. As $\Vert y_n\Vert _H$ is bounded,

$$\begin{aligned} {|}f'_{\lambda _n}(y_n)(y_n-y)| \le \varepsilon _n\Vert y_n-y\Vert \rightarrow 0. \end{aligned}$$

Moreover, as $g'$ is bounded, the uniform convergence of $y_n\rightarrow y$ implies that the second term of $f'_{\lambda _n}(y_n)(y_n-y)$ tends to 0, and hence

$$\begin{aligned} \int _0^{2\pi } y_n'(y_n'-y')\; \hbox {d}t\rightarrow 0. \end{aligned}$$

Then, as $y_n\rightarrow y$ weakly in H, we conclude that

$$\begin{aligned} \int _0^{2\pi } (y_n'-y')^2\; \hbox {d}t\rightarrow 0, \end{aligned}$$

and thus $y_n\rightarrow y$ in H. This proves that $f_\lambda $ satisfies $({\text {PS}})_{\mathbb R,\mathbb R}$.

For $i = -1,1$ we compute

$$\begin{aligned} f_{i}''(0)[v,w] = \int _0^{2\pi } w'(t) v'(t) \hbox {d}t - c a_i \int _0^{2\pi } w(v) v(t) \hbox {d}t. \end{aligned}$$

Writing the elements of H as Fourier series $x(t) = \sum _{n\in \mathbb Z} x_n e^{i n t}$ we have an isomorphism

$$\begin{aligned} H \cong \left\{ (x_n) \in \ell ^2(\mathbb C)\ \bigg /\ \sum _{n\in \mathbb Z} (n x_n)^2 <\infty , x_n = \overline{x_{-n}} \right\} \end{aligned}$$

and in these coordinates

$$\begin{aligned} f_{i}''(0)[v,w] = \sum (n^2 - c a_i) v_n \overline{w_n} \end{aligned}$$

then we have that $\mu (f_i''(0))$ is the number of negative coefficients in the sum, this is

$$\begin{aligned} \mu (f_i''(0)) = \left\{ \begin{array}{ll} 1 + 2 \left\lfloor {\kappa _i}\right\rfloor &{}\quad \text { if}\quad c a_i \ge 0\\ 0 &{}\quad \text {otherwise} \end{array}\right. , \end{aligned}$$

provided $\kappa _i \not \in \mathbb N_0,$ which corresponds to the nondegeneracy of $f_i''(0)$.

Condition 3.4(iii) of Theorem 3.4 can be verified in different ways in terms of g since equation (7.1) is conservative for $\lambda = \pm 1$. For example, assume for simplicity that the area $A(E) = |\{(x,p) \in \mathbb R^2/ \frac{1}{2} p^2 + g(x) \le E\}|$ is a convex function. Then one can check that the minimal period

$$\begin{aligned} T(E) = \sqrt{2} \int _{g(x) \le E} \frac{dx}{\sqrt{E-g(x)}} \end{aligned}$$

of the unique periodic solution $x_E$ of energy E is an increasing function of E (see [4, Chapter 2]). We also have that $T(E) \rightarrow \frac{2\pi }{\kappa _i}$ when $E \rightarrow 0$, so there are at most $ \left\lfloor \kappa _i \right\rfloor $-many periodic solutions of period $2 \pi $, and it suffices to verify that $f_{i}(x_{E}) \ne 0$ if T(E) divides $2 \pi $.

ellerandsor.blogspot.com

Source: https://link.springer.com/article/10.1007/s10231-018-0797-x

Banach Space Prove That There is No Continuous Path That Connects T With the Identity Operator

Introduction

Theorem A

Theorem B

Preliminaries

Lemma

Theorem 2.1

Theorem 2.2

Main results

Definition 3.1

Definition 3.2

Theorem 3.3

Theorem 3.4

Example 3.5

Deformation theorems

Lemma 4.1

Proof

Lemma 4.2

Proof

Lemma 4.3

Remark 4.4

Proof

Theorem 4.5

Proof

Theorem 4.6

Proof

Proofs of Theorems 3.3 and 3.4

Lemma 5.1

Proof

Lemma 5.2

Proof

Proof of Theorem 3.3

Proof of Theorem 3.4

Strongly indefinite functions

Theorem 6.1

Lemma 6.2

Proof

Lemma 6.3

Proof

Lemma 6.4

Proof

Proof of Theorem 6.1

Example of application in a second-order ODE

0 Response to "Banach Space Prove That There is No Continuous Path That Connects T With the Identity Operator"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel